Car Talk
So my friend Brian and I were talking the other day about his car. This is not unusual. It is, after all, a nice car. Actually, it's a Tesla Model S, so beyond being nice it is also the type of car that people who enjoy modeling in Excel can talk about in terms of physics-y stuff too. One thing he mentioned is that he could get a much better charge from a 240V plug than a 120V plug. The difference was something like 26 miles per hour.Here is where it makes it a much better story if I lie and say we were in the car at the time driving 26 miles per hour. We weren't, though. It's too bad. It would have made it an excellent story.
Anyways, I was confused.
"You can measure your car charge in miles per hour?" I asked dubiously. He explained that the car has a similar efficiency curve to a gas car, where as you go faster you get worse "milage", but that the onboard computer could easily figure out your average driving style and with whatever charge you had on your battery give you an approximate number of miles you could travel. Apparently you don't think of your car as half-full of charge, but rather that you have ~150 miles of charge left. Well, the same type of thinking works when you charge the battery up. You don't think about how you are filling it up overnight, but that you are adding ~200 miles of charge. If you do that in 10 hours, you are charging at 20 miles per hour.
This obviously breaks down near the edges. A battery that is almost fully charged will charge more slowly. Driving very slowly and very fast both ruin efficiency, as does cold weather. As does windows down, AC, and for that matter (because the it is not a combustion engine) the heater. Anyways, imagine all that stuff cancels out or doesn't matter.
According to the Tesla website the charging rates are as follows:
120V: 3 mi per charging hour
240V: 29 mi per charging hour
Supercharger: 170 mi in as little as 30 min (much slower thereafter)
Those are all totally drivable speeds (although both 3 mph and 340 mph might get tiring after more than a few minutes). I'm sure there is some technical reason this couldn't be done, probably due to battery magic, err, physics, but a very reasonable way to view this is as an equitemporal pairing. If you drove for one hour at 29 miles per hour you would have to charge one hour at 29 miles per hour to recoup the energy.
Power Ballad
As an aside, you can use this to figure out "How much energy does a Tesla use?"The company states that you can use the 240V, 40 Amp outlet to charge at 29 miles per hour. Some back of the envelope calculations (240 volts x 40 amps = 9.6 kWatt) and (29 mph / 9.6 kW or 29 miles / 9.6 kWh) and you can get about 3 miles per kWh.
As an aside from this aside, if a regular car gets 21 mpg and energy rates stay at about $0.12 per kWh, gas would need to be (21mpg / 3mi x $0.12) $0.92 per gallon to make the cost of driving equal. Interestingly, that is about the (nominal) price of gas in the early 90's when GM pulled the plug on electric cars.
Back to our regularly scheduled aside... But wait! you might say, that is a lot of numbers. How do I know I can trust your math? Good point, hypothetical you. We should come at this from a different direction that doesn't use volts x amps mumbo jumbo. They very explicitly state that you can get in the range of 300 miles from their larger sized battery. This battery happens to be called the 85 kWh battery. Assuming they didn't wildly misname it, you should be able to get (300 miles / 85 kWh = 3.6 miles / kWh). So pretty close.
Sun Roof
So where was I going with that aside? No clue. Didn't even really need Excel. Ah, but you read it anyways, so we should probably do something with that. How about this: we've been assuming that you charge from a wall outlet, but what about solar panels? Aren't they the future? What would happen if you could collect all the sun's energy that radiates down on a certain area (conveniently about 1 kW per square meter) and used it to power a Tesla? You would get about 3 miles of driving per m^2 of perfectly efficient solar panel per hour of sunlight. Thats right, if you put up perfect solar panels on the roof of your 1000 sq ft one-story house, your roof conceivably could be described as 276 miles per hour (Tesla model S miles per hour to be exact).Wow. Brian might be able to make use of that, but I certainly can't drive that fast. But here is an idea that might work- charge the car off of it's parking spot. A car is either driving or it is parked. The more it drives, the more power it needs, and also the more its parking spot is vacant. Can you get the power for driving just from the parking spot it vacated? (For this exercise, assume that most driving, and therefore most solar charging, happens during the day.) A parking spot is roughly (2 m x 5 m) 10 m^2, and therefore could be charging at 10 kW per hour of time that it was not covered by the car. The car could go 30 miles per each hour of charge. If you never break 30 mph, you will always have enough solar panel charge when you get home to get your battery back to full. (If you take this one step further and use the same 10 m^2 of solar panels, but give the car much less "getupandgo" such that it uses less energy and can go 500 miles, you'd pretty much have this.) Improve the solar panels to 100%, stick them on the car itself, and you'd be driving around that racetrack at 15 mph indefinitely, without the tether to a power outlet.
So it is kind of quaint that you can measure both driving and charging in miles per hour, but can we extrapolate this to anything else?
Apologies, and Not For My Puns This Time
So, I guess I have some 'splaining to do with the whole 11-months-between-posts thing. The thing is, I got a new job where I get paid to do science! While this is great for many reasons, the one thing it shorts me on is free time. I might try to fit in a few shorter blog entries and also space things out more evenly, but bear with me if I miss a few months.So, with that out of the way. Lets figure out a way to use mph to figure out how much I get paid!
The main idea here is that there is a limited range of money someone could be paid for work. (Lets say that this is $1-100,000,000 per year, or about 8 orders of magnitude. More realistically people make between $20k and $200k, or just 1 order of magnitude.) Depending on your diet, this will buy a certain number of calories. If you subtract your basal metabolism (needed for survival), you get an excess number of calories. What do we do with these calories? We walk miles! If you are paid hourly, then you are paid in possible walking miles per hour!
This is about to (as I found out while researching it) get very complicated, so lets go stepwise in building our model. First we need our initial inputs. The obvious one is wage. And here we hit our first stumbling block. If you work hourly, you probably know your hourly wage, but if you are salaried, it can be convoluted. If you work 40 hours a week for a year (52 weeks) you end up putting in a nice-and-close-to-round 2080 hours which lends itself to this rule of thumb: divide your salary (in thousand $'s) by 2 and it is your hourly wage... almost. It will always be (2080/2000) 4% too high. If you take two weeks of vacation it is exact. But many people don't work 40 hours a week, so for them I made this handy chart:
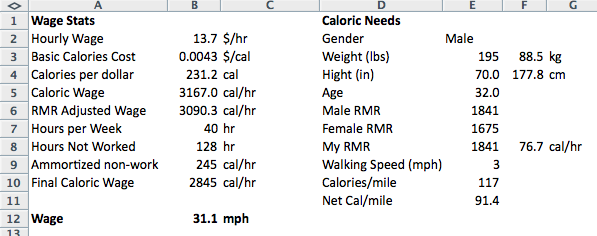
While we are plugging in numbers, let's use the annual median income of $28,500 (as of 2012) which we can enter as $13.70 per hour. Yay data! Leave some space for labeling things, and add [13.70] value to cell B2. (For those of you new to the blog, things [in brackets] should be entered in Excel.)
How many calories is that? The average American spends a little over $6k a year to consume 3800 calories a day. I know. That means calories cost (cell B3 [=6000/(365*3800)]) $0.0043, or about (cell B4 [=1/B3]) 233 calories per dollar. (As a sanity check this value kind of makes sense. One dollar of candy bar might have more calories, but one dollar of lettuce will have fewer.) Of course this will change with individual diets, but this means that our caloric wage is (cell B5 [=B2*B4]) 3167 calories per hour. An average American could probably survive on 1 hour of work a day to buy their food if all their other needs were provided for. This fits with the statistic that the average American spends around 12% of their income on food (although this varies widely at the outer quintiles of the wage range).
But how much of that is excess? To figure that out we need to find out how many calories we burn in an hour of doing nothing (aka resting metabolic rate, or RMR). This depends on several factors, is empirically determined, and is a different equation for male or female. Enter the following:
Cell E2: Gender
Cell E3: Weight (lbs.) Cell F3: [=0.4536*E3] kg
Cell E4: Height (inches) Cell F4: [=2.54*E4] cm
Cell E5: Age
Male RMR (cell E6): =(F3*10+F4*6.25-5*E5+5)
Female RMR (cell E7): =(F3*10+F4*6.25-5*E5+5)
My RMR (cell E8): =IF(E2="Male",E6,E7)
Hopefully I haven't lost you yet. Basically, the equation says that the heavier, taller, and younger you are, the more calories your body burns to stay alive. For some reason women also burn fewer calories even holding the rest of that constant. As an aside, oxidative metabolism produces radical species that are a component of aging. Is this an aspect of why women live longer than men? This is the type of coincidence I'd love actually assign a correlation to... but not for this (already way too late in coming) post!
So if we throw in some numbers for a 32y/o male who is the average American weight (195 lbs) and height (5'10" = 70 inches), their RMR is 1841 calories a day, or (cell F8 [=F7/24]) about 77 calories per hour. Their caloric wage accrual rate is actually now only (cell B6 [=B5-F8]) 3015 calories per hour. This resting metabolism only takes up 2-3% of your wage!
Ok, one more aside. Imagine you were a hunter gatherer picking, oh, I don't know... blueberries (which have about 0.78 calories each). You would need to consume 100 blueberries an hour to satisfy your RMR. That need would increase as you spent energy picking. You would need 4872 blueberries a day consume an average American diet of calories. If you wanted "to make the average median income" in calories, you would need to pick just over a berry per second. As anyone who has gone berry picking knows, that is easy to do for a few minutes but very hard to sustain for an hour (let alone 8 hours!) It kind of puts it into perspective that not only was it hard for a nomadic people to maintain and transport a surplus, but it probably wasn't practical to form one in the first place!
So back to the mph wage. We now have two values of caloric wage that could be converted to walking miles. The values aren't that different, but just different enough that we should probably try to choose the adjusted one. After all, that would be the more overly complicated choice. The biggest complication there is that your RMR is a constant need, but work is not constant. If someone works one hour a week, they still have the RMR to fulfill for the entire week. For the man working the median income wage ($13.7 an hour) the surplus calories from work will be a function of the amount of time worked. It would look something like this:
To build in this adjustment, we need to tweak the wage one more time. For this we must know how many hours per week you work (cell B7) and don't work (cell B8 [=24*7-B7]), plus how many calories per hour you need to make up for the hours you aren't working (cell B9 [=B8*F8/B7]). If we subtract that from the RMR wage, we get the full adjustment (cell B10 [=B6-B9]). For our average guy, the numbers might be 40 hrs per week worked, 128 hours per week not worked, resulting in a 245 cal/hr deduction to make up for the unworked time. His final caloric wage is 2845 cal/hr.
So let's use those calories!
Walka Walka Walka
It turns out that walking is complicated! While running (on flat ground), the caloric cost is independent of pretty much everything except how long you do it and how heavy you are. (You are basically jumping up and down repeatedly.) Walking is different. It still depends on how heavy you are, how long you do it and the gradient, but it also depends on the speed of the walking... with linear, quadratic, and cubic components! Walking very fast (> 5 mph) can even burn more calories than running. Its hard to do, and even speed walkers rarely get to 10 min miles. Additionally, all the equations for caloric cost break down at the extremes of the velocity spectrum, so lets preempt those problems and ask people how fast they walk (cell E9) and use data validation to constrain it to 0.5 to 5 mph where the equations are mostly linear with weight and time.
Cell E10 = 0.6*E3
Our average 195 lb guy burns about 118 calories per mile. This agrees with many of the online calculators out there, but this value is still describing gross calories burned. For the net calories per mile will need to subtract out what he would have burned anyways in that amount of time (the hours per mile). So when we account for this (cell E11 [=E10-F8/E9]) we find out that his calories per mile is quite variable. If he walks 3 mph, his calories per mile is reduced to 91 calories per mile.
Putting it All Together
So now that we have all the components, lets figure out what this average man's wage is in miles per hour. With their physical characteristics, working a 40 hour workweek, and walking 3 mph, they get paid (cell B12 [=B10/E11]) 31 mph.Cool! How does it vary if he changes weight? Losing 20 lbs could actually earn him an extra 15% raise.
And what about gender inequality? If we had an average woman (5'4", 165 lbs) instead of an average man, we make some steps in the right direction. Other takeaways are that additional height has a very small positive impact on your wage and additional age has a very small negative one. Walking very slowly does help, but you'd run out of time to do your walking!
And of course, as always, you have to make wise food choices.
-----
Have an interesting idea you want modeled? Didn't answer your burning question about a random topic? Think I did my math wrong? Let me know in the comments! If you want to get email notifications when new posts go up, send an email to subscribe+overly-complicated-excel@googlegroups.com to subscribe to the mailing list. Also, you can click the link in the right hand sidebar.